About Dynamic Programming

DP = Recursion + Memorization

What is DP?

DP is firstly introduced by Richard E. Bellman in 1953. A problem is broken down into sub-problems, the results are saved, and then the sub-problems are optimized to find the overall solution. It often appears with a constraint, when you try to optimize something with a constraint.

About DP

• DP is useful when you're trying to optimize something given a constraint.
• You can use dynamic programming when the problem can be broken into discrete subproblems.
• Every DP involves a grid. Draw the grid, think about what will be the row and col of this grid? the constraint and the solution?
• The values in the cells are usually what you're trying to optimize.
• Each cell is a subproblem, so think about how you can divide your problem into subproblems. What does the value of the cell represent?

Exercises in Hackerrank

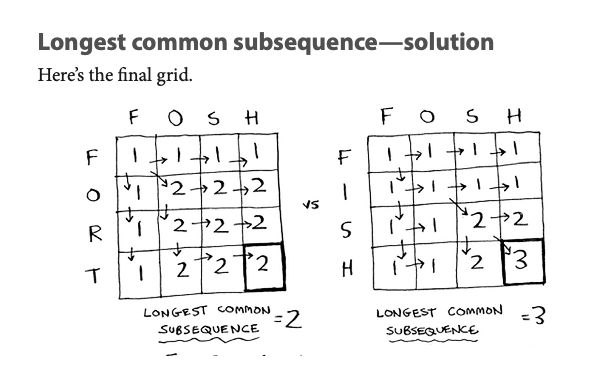
• The Longest Common Subsequence
  Problem link. Here, dp[i][j] represents the length of the longest common subsequences between the first i elements of list a and the first j elements of list b. The reasoning behind the line dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]); is as follows:

  • If the last elements of both lists (a.get(i - 1) and b.get(j - 1)) are equal, then we extend the LCS by one, and dp[i][j] is set to dp[i - 1][j - 1] + 1.
  • If the last elements of both lists are not equal, then we need to consider two cases:
    • If we exclude the last element of list a, then the LCS remains the same as the LCS between the first i - 1 elements of list a and the first j elements of list b, i.e., dp[i][j] = dp[i - 1][j].
    • If we exclude the last element of list b, then the LCS remains the same as the LCS between the first i elements of list a and the first j - 1 elements of list b, i.e., dp[i][j] = dp[i][j - 1]. So, dp[i][j] is set to the maximum of these two values because we want to find the longest common subsequence. If either of the lists has a longer common subsequence without including the current element (a.get(i - 1) or b.get(j - 1)), we take that value. This ensures that dp[i][j] contains the length of the longest common subsequence up to the ith element of list a and the jth element of list b.

    public static List<Integer> longestCommonSubsequence(List<Integer> a, List<Integer> b){
        int m = a.size();
        int n = b.size();
  
        int[][] dp = new int[m+1][n+1];
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <=n; j++){
                if(a.get(i-1).equals(b.get(j-1))){
                    dp[i][j] = dp[i-1][j-1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
                }
            }
        }
  
        List<Integer> lcs = new ArrayList<>();
        int i = m, j = n;
        while(i > 0 && j > 0){
            if(a.get(i-1).equals(b.get(j-1))){
                lcs.add(a.get(i-1));
                i--;
                j--;
            } else if(dp[i-1][j] > dp[i][j-1]){
                i--;
            } else {
                j--;
            }
        }
        Collections.reverse(lcs);
        return lcs;
    }
  

• The Maximum Contiguous Subarray
  Problem link. Kandane's algorithm. O(n) time, O(1) space.

  def max_subarray(numbers):
    """Find the largest sum of any contiguous subarray."""
    best_sum = - infinity
    current_sum = 0
    for x in numbers:
        current_sum = max(x, current_sum + x)
        best_sum = max(best_sum, current_sum)
    return best_sum
  

  public static List<Integer> maxSubarray(List<Integer> arr) {
        int currentSum = arr.get(0);
        int maxSum = arr.get(0);
  
        for (int i = 1; i < arr.size(); i++) {
            int num = arr.get(i);
            currentSum = Math.max(num, currentSum + num);
            maxSum = Math.max(maxSum, currentSum);
        }
  
        List<Integer> res = new ArrayList<>();
        res.add(maxSum);
        Collections.sort(arr);
        Collections.reverse(arr);    
  
        int sum = arr.get(0);
        for(int i = 1;i<arr.size();i++){
            sum = Math.max(sum, sum+arr.get(i));
        }
        res.add(sum);
        return res;
    //return the maximum subarray and subsequence sums
  }