Learn Recursion recursively... Understanding recursion is about understanding recursion...

In order to understand recursion, one must first understand recursion

`Break one big problem into smaller, similar sub-problems`

Ironically, I learn about Recursion recursively... (first time I realize this). No matter how many times (4 times) I learned about recursion, I still get intimidated when I see one recursion problem, so I have to go back and learn it again. What's wrong? I think the reason is both a lack of practice and a deep understanding. This time I decided to dig deeper and merge this concept thoroughly in my mind. Before everything, I want to share a well-explained video about recursion.

History

The concept of recursion has been present in mathematics (in ancient times) and computer science for many centuries. The most known ones are Euclidean Algorithm, Fibonacci Sequences, Pacal's Triangle, Edsger Dijkstra chronological. Now, recursion is commonly used to solve problems like tree traversal, searching, sorting, and mathematical calculations. And we also use recursive algorithms solve great amount of LeetCode questions, including Arrays and Strings, Linked Lists, Trees and Graphs, Recursion, Dynamic Programming, Binary Search, Backtracking and so on. So if you don't know about Recursion well, the interview is done.

Known Recursion

Euclidean Algorithm

Fibonacci Sequences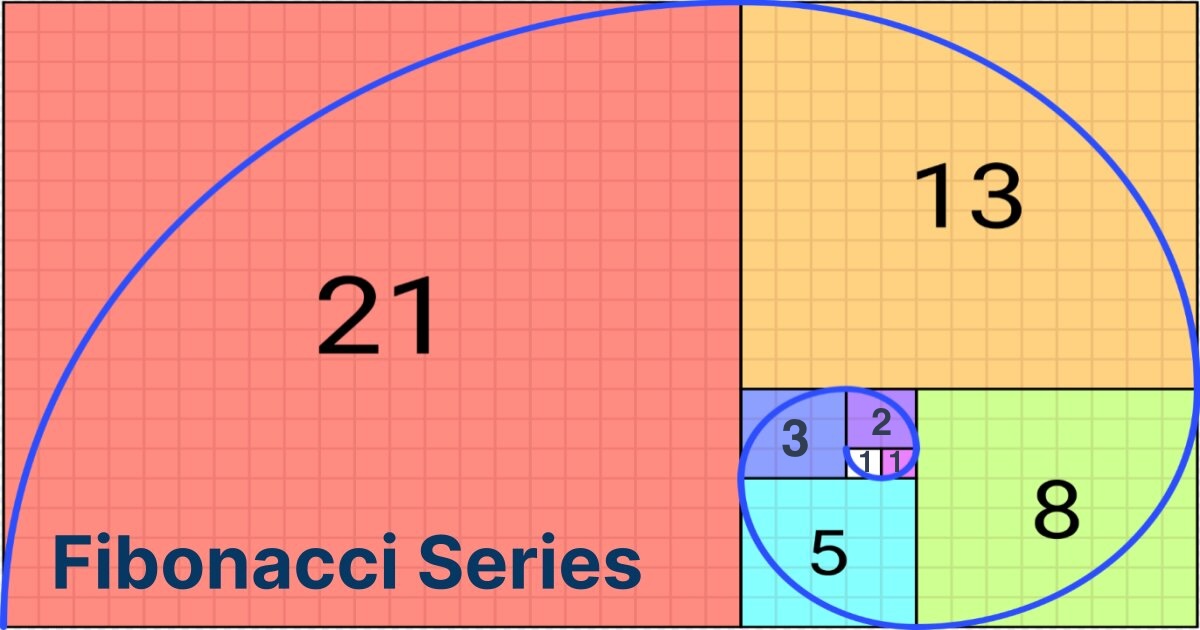

public class Fibonacci {
  public static void main(String[] args) {
      int n = 10; //  n: Fibonacci number index
      int result = fibonacci(n);
      System.out.println("The " + n + "th Fibonacci number is: " + result);
  }

  // Recursive method to calculate the nth Fibonacci number
  public static int fibonacci(int n) {
      if (n <= 1) {
          return n;
      } else {
          return fibonacci(n - 1) + fibonacci(n - 2);
      }
  }
}

Pacal's Triangle
Compare the difference between Pascal Triangle and Fibonacci Sequences. What you got in common? In these two patterns, the latter appeared element is the sum of two other previously appeared elements. Fibonacci Sequences is easier, we can represent it in one line, one dimension. While Pascal Triangle is a bit more complex, it's a traingle! we can represent it in two dimensions. So what would the data look like? We can row and col.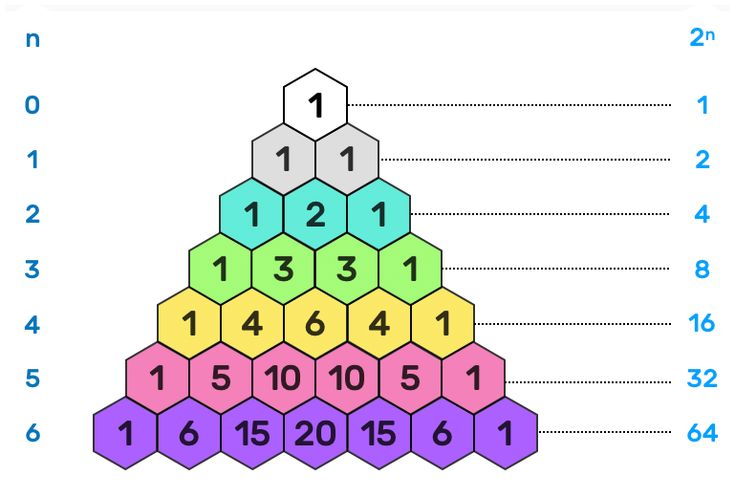

public class PacalTriangle {
  public static int pascalValue(int row, int col){
      if(col == 0 || col == row){
          return 1;
      } else {
          return pascalValue(row - 1, col -1) + pascalValue(row - 1, col);
      }
  }
  public static void printPascalTriangle(int numRows){
      for(int i = 0; i < numRows; i++){
          for(int j = 0; j <= i; j++){
              System.out.print(pascalValue(i, j) + " ");
          }
          System.out.println();
      }
  }

  public static void main(String[] args){
      int numRows = 5;
      printPascalTriangle(numRows);
  }
}

Edsger Dijkstra
Dude is a great Dutch computer scientist, check out his paper on Recursive Programming. Dijkstra's algorithm finds the shortest path.

import java.util.*;

public class DijkstraAlgorithm {

  static class Edge {
    int to, weight;

    public Edge(int to, int weight) {
        this.to = to;
        this.weight = weight;
    }
  }

  public static void dijkstra(List<List<Edge>> graph, int source) {
    int n = graph.size();
    int[] dist = new int[n];
    Arrays.fill(dist, Integer.MAX_VALUE);
    dist[source] = 0;

    PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[1]));
    pq.offer(new int[]{source, 0});

    while (!pq.isEmpty()) {
        int[] curr = pq.poll();
        int u = curr[0], distance = curr[1];

        if (distance > dist[u]) continue; // Skip if outdated distance

        for (Edge edge : graph.get(u)) {
            int v = edge.to, weight = edge.weight;
            if (dist[u] + weight < dist[v]) {
                dist[v] = dist[u] + weight;
                pq.offer(new int[]{v, dist[v]});
            }
        }
    }

    // Print the shortest distances from source to all nodes
    System.out.println("Shortest distances from source " + source + ":");
    for (int i = 0; i < n; i++) {
        System.out.println("Node " + i + ": " + dist[i]);
    }
  }

  public static void main(String[] args) {
    int n = 5; // Number of nodes
    List<List<Edge>> graph = new ArrayList<>();
    for (int i = 0; i < n; i++) {
        graph.add(new ArrayList<>());
    }

    // Add edges to the graph
    graph.get(0).add(new Edge(1, 4));
    graph.get(0).add(new Edge(2, 2));
    graph.get(1).add(new Edge(2, 5));
    graph.get(1).add(new Edge(3, 10));
    graph.get(2).add(new Edge(3, 3));
    graph.get(3).add(new Edge(4, 7));

    int source = 0; // Source node
    dijkstra(graph, source);
  }
}

Recursion Function

Every recursion function has two part, base case and recursive case. Recursive case refers when function call itself, base case refers when function stop calling itself, so that it won't end up in infinite loop. (think about stack)

General Approach

Identify edge case:
Break down the problem:
Recursive call:
Combine results:
Handle base cases:

Exercises

Tree Traversal

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(){}
    TreeNode(int v){
        val = v;
    }
    TreeNode(int v, TreeNode r, TreeNode l){
        val = v;
        right = r;
        left = l;
    }

    public List<Integer> preorderTraversal(TreeNode root){
        List<Integer> list = new ArrayList<>();
        preorder(root, list);
        return list;
    }
    public void preorder(TreeNode root, List<Integer> result){
        if(root == null) return;
        result.add(root.val);
        preorder(root.left, result);
        preorder(root.right, result);
    }
}

Backtracking -> Graphs -> DP

DP = Recursion + Memorization

A great video explanation about DP.

Backtracking

Backtracking algorithm works by recursively exploring all possible solutions to a problem. It starts by choosing an initial solution, and then it explores all possible extensions of that solution. If an extension leads to a solution, the algorithm returns that solution. ??? what to remember between each recursion? the argument in the function. think of a tree structure.

Combinations
Sorting

Index